「人生どのタイミングで結婚相手を決めるべきか？」を数学的に解明する Secretary Problem

Share

12 件

いいね！

付き合える最大人数を3人で考えるとわかりやすい

前述のWashington Postの記事の中に、付き合える最大人数を3人にした場合の確率図があります。

• これから3人の人とお付き合いできる可能性がある
• 3人には1位、2位、3位という明確な優劣があるとする
• その中から結婚相手を選ぶ
• 1位、2位、3位の人と付き合う順番はランダム
• 1位を選びたい

という条件だとすると以下の組み合わせが出てきます。順列組み合わせの問題みたいですが、

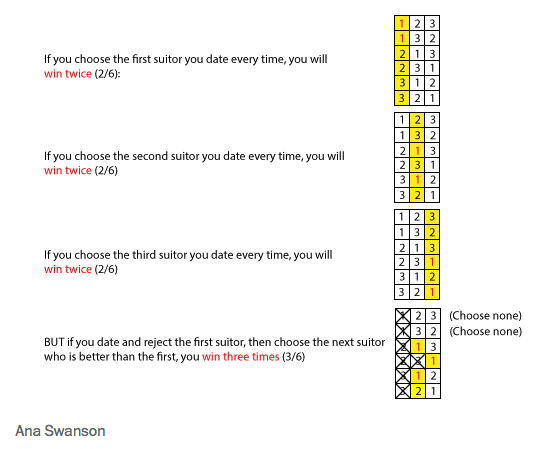
image by：TED Talk

最初にお付き合いした人で決める場合、1位の人を選択できる確率は2/6＝33%
2番目にお付き合いした人で決める場合、1位の人を選択できる確率は2/6＝33%
3番目にお付き合いした人で決める場合、1位の人を選択できる確率は2/6＝33%

1番目にお付き合いした人を基準とし、その次にそれを上回る人を選んだ場合に1位の人を選択できる確率は、3/6なので50%

確率があがっている！

まあでも現実はそうもいかない

まあとはいえ、前提条件がなかなか難しいですよね。

「一定期間付き合った後、結婚するか・別れるかの判断をするものとする」…なかなか決められなくてズルズルしちゃったりしますし。

「その人と結婚するかは、それまで付き合った人との相対的順位にのみ基づいて決定する」…いやいや、必ずしも相対的順位が付けられるものではないし。この人にも、あの人にもそれぞれ比べられない良い所があるのよ。

「一度別れた人とよりを戻すことはできない」…意外とがんばってよりを戻そうとしたりしちゃったり。

「こちらが結婚を決めたら相手は決して断らない」…こちらが決めても相手がその気じゃないこともありますし。。

ということで、まああくまで参考程度の話ですが、なんか面白かったのでブログにまとめてみました。

TED Talk「The mathematics of love」ではこの他にも「数学的に使える愛のTips」が2つ紹介されていたので、興味がある方は動画を見てみてください。

• image by：Unsplash
• source:『Be Magnetic!』人生どのタイミングで結婚相手を決めるべきか？を数学的に解明する Secretary Problem （記事タイトル・本文見出しはMONEY VOICE編集部）
• ※初出：MONEYVOICE（2017/12/24）
• ※掲載時の情報です。内容は変更になる可能性があります。